什么是合数目录K8D高三网

什么是合数K8D高三网

合数是什么？K8D高三网

什么是合数?K8D高三网

什么是合数

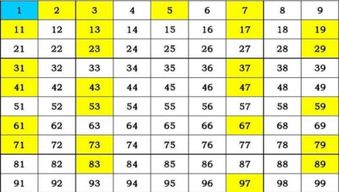
    合数是一个数学概念，是指大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。例如，4、6、9和10都是合数，因为它们都有除了1和本身之外的其他因数。与之相对的是质数，质数是只有两个正因数（1和本身）的自然数。合数是一种数字分类基础概念，属于自然数的范畴。合数也可以通过计算其质因数的个数来进行分类，例如有两个质因数的合数称为半质数，有三个质因数的合数则称为楔形数。在某些应用中，还可以将合数分为有奇数个质因数的合数和有偶数个质因数的合数。K8D高三网

合数是什么？

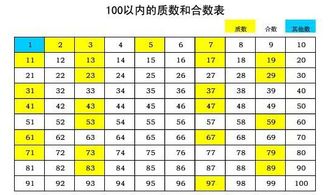
合数是与质数相对应的概念。K8D高三网

只能被1和自身所整除的数叫质数。K8D高三网

如：2、3、5、7、11等。K8D高三网

其它不仅能被1和自身整除还能被其它数整除的数叫合数。K8D高三网

如：4、6、8、9、10、12等。K8D高三网

另外，讨论合数与质数必须在大于等于2的整数范围内。K8D高三网

什么是合数?

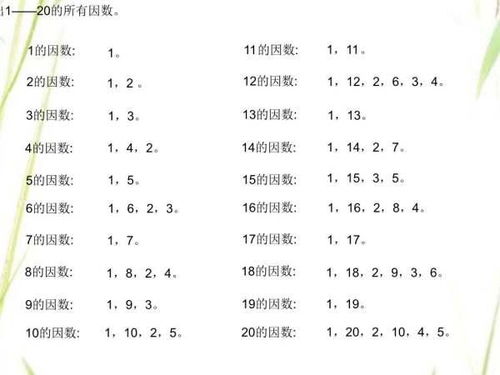
　在自然数中，我们将那些可以被2整除的数叫作偶数，如K8D高三网

　　2、4、6、8、10、...K8D高三网

等，剩下的那些自然数就叫作奇数，如K8D高三网

　　1、3、5、7、9、...K8D高三网

等。K8D高三网

这样，所有的自然数就被分成了偶数和奇数两大类。K8D高三网

另一方面，除去1以外，有的数除了1和它本身以外，不能再被别的整数整除，如K8D高三网

　　2、3、5、7、11、13、17、...K8D高三网

等，这种数称作素数(也称质数)。K8D高三网

有的数除了1和它本身以外，还能被别的整数整除，这种数就叫合数，如K8D高三网

　　4、6、8、9、10、12、14、...K8D高三网

等，就是合数。K8D高三网

1这个数比较特殊，它既不算素数也不算合数。K8D高三网

这样，所有的自然数就又被分为1和素数、合数三类。K8D高三网

自然数的这种分类法，要比它分为奇数和合数两大类要复杂多了。K8D高三网

　　对于素数这个概念，我们自然会想到这样一个问题：怎样从自然数集合中找出素数？素数到底有多少个？K8D高三网

　　假设给定一个自然数N，要求出N以内的所有素数，可以这样进行：因为N以内的自然数只有三种，一种是1，一种是合数，一种是素数；我们可以象筛东西那样，先把1筛掉，然后再把合数筛掉，剩下的就是素数了，这种在自然数列中寻找素数的方法就叫做埃拉托色尼筛法(简称埃氏筛法)。K8D高三网

　　用筛法找出不超过N的全部素数，可以遵循下面的定理进行。K8D高三网

　　辅助定理1：“如果n是不大于x的合数，那么n必有一个不大于√x的素约数(符号“√”表示开平方)”(证从略)。K8D高三网

根据辅助定理1，我们只要用不大于√x的素数作筛子，就可将不大于X以内的所有的合数筛除掉。K8D高三网

　　辅助定理2：“素数有无限多个”(证从略)。K8D高三网

　　虽然素数有无穷多个，但在自然数列中的一个相当长的数列中，却找不到一个素数，而有时会出现若p是素数，p+2也是素数的情况，所以素数的出现并无规则可言。K8D高三网

　　一个素数只有1和本身这两个约数，因此素数就不能再分解了。K8D高三网

但是合数却有两个以上的素约数，那么合数能不能分解成约数全部是素数的乘积呢？答案是肯定的。K8D高三网

　　唯一分解定理：“任何大于1的自然数都可以分解成素数的乘积，如果不计较这些素因数的顺序，这种分解方法是唯一的”(证从略)。K8D高三网

　　根据唯一分解定理，欲求某自然数的倍数之数列，只要用该数乘以自然数列，即可得到该数的倍数之数列。K8D高三网

由此可知，合数的出现是有规则可言的。K8D高三网

埃氏筛法就是根据合数的出现是有规则可言的基础上，逐个地将不大于√x的素数的倍数筛掉。K8D高三网

根据辅助定理1，可知，筛掉那些具有不大于√x素约数的合数，序列中已无合数的存在，剩下的就是大于√x至x的素数了。K8D高三网

　　在运用筛法时，就可发现，当筛除某数的倍数时，有时会遇到数列中的数已被前一个筛子所筛，这样就会造成计算上的误差。K8D高三网

针对此种情况，在数论有一个逐步淘汰原则：K8D高三网

　　“设有N件事物，其中，N_i件有性质i，N_j件有性质j, ..., N_ij件兼有性质i及j，...，N_ijk件兼有性质i、j及k，...。K8D高三网

则此事物中之既无性质i，又无性质j，又无性质k，...者之件数为K8D高三网

　　N-N_i-N_j-N_k-...+N_ij+...-N_ijk-...+...-...。K8D高三网

”①。K8D高三网

　　根据埃氏筛法和逐步淘汰原则，数论创建了求不大于X以内的素数之函数π(x)。K8D高三网

所谓的π(x)函数，是指：K8D高三网

　　π(x)=N-r-1-{r∑i=1}[N/pi]+{∑1≤ii*pj]-...K8D高三网

　　+(-1)r[N/pi*pj*...*pr]K8D高三网

这是数论中求自然数列中素数的个数问题之唯一的一个根据规律而创建的函数，而所谓的素数定理中的Lix(x)函数仅是由于计算出来的数值有接近于π(x)函数中的数值而被高斯先生提议替代π(x)函数之用。K8D高三网

因为在π(x)函数中的取整之步骤，使得计算成为十分繁琐之事。K8D高三网

但在Lix(x)函数中，并无所求素数的个数之任何规律，在Lix函数中，仅是对数函数的积分，而对数函数只是指数函数的反函数也。K8D高三网

标签：