导数公式及运算法则是什么目录yxT高三网

导数公式及运算法则是什么yxT高三网

高中导数公式yxT高三网

求导公式运算法则yxT高三网

求导公式运算法则是什么？yxT高三网

导数公式及运算法则是什么

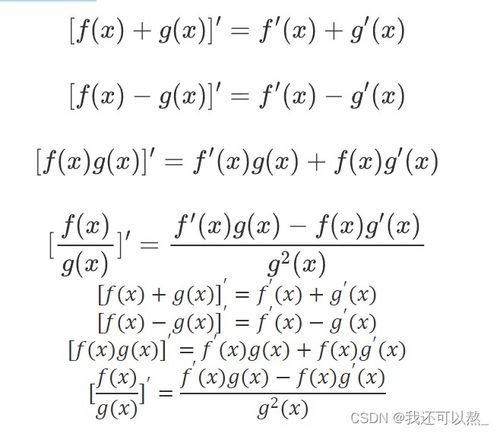
① C'=0(C为常数函数) yxT高三网

　　② (x^n)'= nx^(n-1) (n∈Q*)；熟记1/X的导数 yxT高三网

　　③ (sinx)' = cosx yxT高三网

　　(cosx)' = - sinx yxT高三网

　　(tanx)'=1/(cosx)^2=(secx)^2=1+(tanx)^2 yxT高三网

　　-(cotx)'=1/(sinx)^2=(cscx)^2=1+(cotx)^2 yxT高三网

　　(secx)'=tanx·secx yxT高三网

　　(cscx)'=-cotx·cscx yxT高三网

　　(arcsinx)'=1/(1-x^2)^1/2 yxT高三网

　　(arccosx)'=-1/(1-x^2)^1/2 yxT高三网

　　(arctanx)'=1/(1+x^2) yxT高三网

　　(arccotx)'=-1/(1+x^2) yxT高三网

　　(arcsecx)'=1/(|x|(x^2-1)^1/2) yxT高三网

　　(arccscx)'=-1/(|x|(x^2-1)^1/2) yxT高三网

　　④(sinhx)'=coshx yxT高三网

　　(coshx)'=sinhx yxT高三网

　　(tanhx)'=1/(coshx)^2=(sechx)^2 yxT高三网

　　(coth)'=-1/(sinhx)^2=-(cschx)^2 yxT高三网

　　(sechx)'=-tanhx·sechx yxT高三网

　　(cschx)'=-cothx·cschx yxT高三网

　　(arsinhx)'=1/(x^2+1)^1/2 yxT高三网

　　(arcoshx)'=1/(x^2-1)^1/2 yxT高三网

　　(artanhx)'=1/(x^2-1) (|x|<1) yxT高三网

　　(arcothx)'=1/(x^2-1) (|x|>1) yxT高三网

　　(arsechx)'=1/(x(1-x^2)^1/2) yxT高三网

　　(arcschx)'=1/(x(1+x^2)^1/2) yxT高三网

　　⑤ (e^x)' = e^x yxT高三网

　　(a^x)' = （a^x）lna （ln为自然对数） yxT高三网

　　(Inx)' = 1/x（ln为自然对数） yxT高三网

　　(logax)' =x^(-1) /lna(a>0且a不等于1) yxT高三网

　　(x^1/2)'=[2(x^1/2)]^(-1) yxT高三网

　　(1/x)'=-x^(-2) yxT高三网

补充一下。yxT高三网

上面的公式是不可以代常数进去的，只能代函数，新学导数的人往往忽略这一点，造成歧义，要多加注意。yxT高三网

关于三角求导“正正余负”（三角包含三角函数，也包含反三角函数正指正弦、正切与正割。yxT高三网

） yxT高三网

　　(3)导数的四则运算法则(和、差、积、商)： yxT高三网

　　①(u±v)'=u'±v' yxT高三网

　　②(uv)'=u'v+uv' yxT高三网

　　③(u/v)'=(u'v-uv')/ v^2yxT高三网

求导公式运算法则

运算法则yxT高三网

减法法则：(f(x)-g(x))'=f'(x)-g'(x)yxT高三网

加法法则：(f(x)+g(x))'=f'(x)+g'(x)yxT高三网

乘法法则：(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)yxT高三网

除法法则：(g(x)/f(x))'=(g'(x)f(x)-f'(x)g(x))/(f(x))^2yxT高三网

导数公式yxT高三网

1.y=c(c为常数) y'=0yxT高三网

2.y=x^n y'=nx^(n-1)yxT高三网

3.y=a^x y'=a^xlnayxT高三网

y=e^x y'=e^xyxT高三网

4.y=logax y'=logae/xyxT高三网

y=lnx y'=1/xyxT高三网

5.y=sinx y'=cosxyxT高三网

6.y=cosx y'=-sinxyxT高三网

7.y=tanx y'=1/cos^2xyxT高三网

8.y=cotx y'=-1/sin^2xyxT高三网

求导公式运算法则是什么？

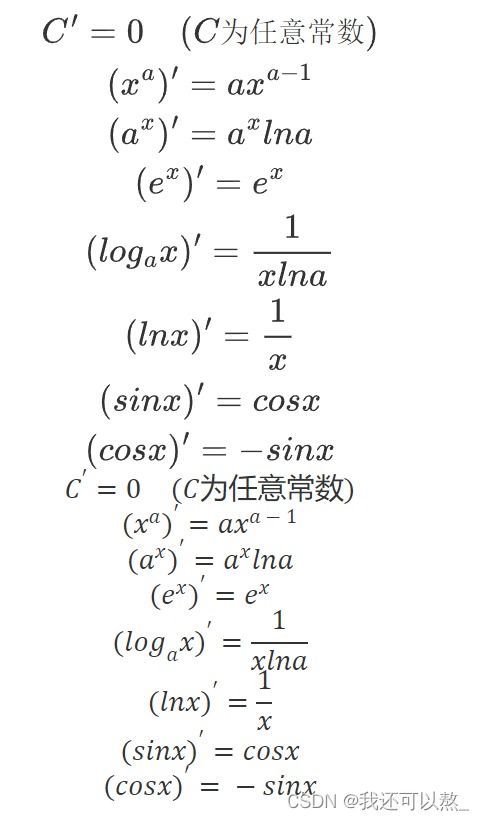
运算法则是：加（减）法则，[f(x)+g(x)]'=f(x)'+g(x)'；乘法法则，[f(x)*g(x)]'=f(x)'*g(x)+g(x)'*f(x)；除法法则，[f(x)/g(x)]'=[f(x)'*g(x)-g(x)'*f(x)]/g(x)^2。yxT高三网

若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。yxT高三网

导数也叫导函数值，又名微商，是微积分中的重要基础概念。yxT高三网

由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。yxT高三网

求导运算法则是：加（减）法则：[f(x)+g(x)]'=f(x)'+g(x)'；乘法法则：[f(x)*g(x)]'=f(x)'*g(x)+g(x)'*f(x)；除法法则：[f(x)/g(x)]'=[f(x)'*g(x)-g(x)'*f(x)]/g(x)^2。yxT高三网

一个函数在某一点的导数描述了这个函数在这一点附近的变化率。yxT高三网

如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。yxT高三网

导数的本质是通过极限的概念对函数进行局部的线性逼近。yxT高三网

例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。yxT高三网

不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。yxT高三网

若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。yxT高三网

然而，可导的函数一定连续；不连续的函数一定不可导。yxT高三网

对于可导的函数f(x)，x?f'(x)也是一个函数，称作f(x)的导函数（简称导数）。yxT高三网

寻找已知的函数在某点的导数或其导函数的过程称为求导。yxT高三网

实质上，求导就是一个求极限的过程，导数的四则运算法则也来源于极限的四则运算法则。yxT高三网

反之，已知导函数也可以倒过来求原来的函数，即不定积分。yxT高三网

微积分基本定理说明了求原函数与积分是等价的。yxT高三网

求导和积分是一对互逆的操作，它们都是微积分学中最为基础的概念。yxT高三网

标签：