辅助角公式目录t9Q高三网

求数学辅助角公式t9Q高三网

辅助角公式是什么？？t9Q高三网

三角函数 辅助角公式t9Q高三网

以下是常用的辅助角公式：nn1. 余角公式：$$sin(frac{pi}{2}-theta)=costheta, quad cos(frac{pi}{2}-theta)=sintheta$$nn2. 和差角公式：$$sin(theta pm phi)=sinthetacosphi pm costhetasinphi$$ $$cos(theta pm phi)=costhetacosphi mp sinthetasinphi$$nn3. 二倍角公式：$$sin2theta=2sinthetacostheta$$ $$cos2theta=cos^2theta-sin^2theta=2cos^2theta-1=1-2sin^2theta$$nn4. 三倍角公式：$$sin3theta=3sintheta-4sin^3theta$$ $$cos3theta=4cos^3theta-3costheta$$nn5. 半角公式：$$sinfrac{theta}{2}=pmsqrt{frac{1-costheta}{2}

求数学辅助角公式

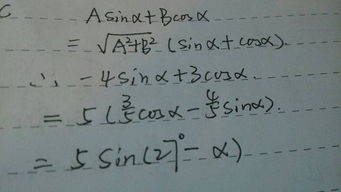
acosx＋bsinx＝√(a^2+b^2)sin(x+arctan(a/b)) 　　这就是辅助角公式． t9Q高三网

证明t9Q高三网

设acosA+bsinA=xsin(A+M) t9Q高三网

　　∴acosA+bsinA=x((a/x)cosA+(b/x)sinA) t9Q高三网

　　由题，（a/x)^2+(b/x)^2=1,sinM=a/x,cosM=b/x t9Q高三网

　　∴x=√(a^2+b^2) t9Q高三网

　　∴acosA+bsinA=√(a^2+b^2)sin(A+M) ,tanM=sinM/cosM=a/bt9Q高三网

辅助角公式是什么？？

对于acosx+bsinx型函数，我们可以如此变形acosx+bsinx=Sqrt(a^2+b^2)(acosx/Sqrt(a^2+b^2)+bsinx/Sqrt(a^2+b^2))，令点(b,a)为某一角φ终边上的点，则sinφ=a/Sqrt(a^2+b^2),cosφ=b/Sqrt(a^2+b^2)t9Q高三网

∴acosx＋bsinx＝Sqrt(a^2+b^2)sin(x+arctan(a/b))t9Q高三网

这就是辅助角公式． t9Q高三网

设要证明的公式为asinA+bcosA=√(a^2+b^2)sin(A+M) (tanM=b/a) t9Q高三网

以下是证明过程： t9Q高三网

设asinA+bcosA=xsin(A+M) t9Q高三网

∴asinA+bcosA=x((a/x)sinA+(b/x)cosA) t9Q高三网

由题，（a/x)^2+(b/x)^2=1,sinM=a/x,cosM=b/x t9Q高三网

∴x=√(a^2+b^2) t9Q高三网

∴asinA+bcosA=√(a^2+b^2)sin(A+M) ,tanM=sinM/cosM=b/at9Q高三网

三角函数 辅助角公式

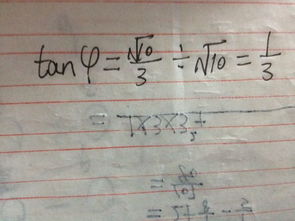
用化一公式 asinx+bcosx=根号下(a^2=b^2)sin(x+w) tanw=b/a 根据坐标（a,b）判断角在那一象限 a,b要带符号

标签：